|
|
马上注册,结交更多好友,享用更多功能,让你轻松玩转社区。
您需要 登录 才可以下载或查看,没有账号?注册

×
作者:微信文章
朴素贝叶斯(naïve Bayes)算法是基于特征条件独立性假设的分类方法。尽管这一假设在多数现实场景中并不完全成立,但朴素贝叶斯仍能在大量分类任务中展现出优异性能,尤其在文本分类、垃圾邮件过滤、情感分析等文本分析问题中获得了广泛应用,此外还常用于医学诊断、推荐系统等领域,凭借简洁的逻辑和高效的计算成为机器学习中的经典算法。
朴素贝叶斯模型
假设训练集 包含 个样本,每个样本 是 维特征向量, 为特征维度,类标签 , 为类别总数。设随机变量 表示输入特征, 表示类别变量,朴素贝叶斯的核心目标是对给定的测试样本 ,计算其属于每个类别的后验概率,选择概率最大的类别作为预测结果。
这一核心逻辑基于贝叶斯定理,样本 属于类别 的后验概率可表示为:
对任意测试样本 ,证据概率 是与类别无关的常数,同一组特征的边际概率固定,因此后验概率的大小比较可忽略分母,简化为:
根据条件独立性假设,给定类别标签 的条件下各特征相互独立,因此联合条件概率可拆解为单个特征条件概率的乘积,大幅简化计算:
综合上述简化公式,朴素贝叶斯的最终预测准则为选择使先验概率×特征条件概率乘积最大的类别作为预测结果:
其中 为测试样本 的预测类别。
朴素贝叶斯的参数估计核心是求解先验概率 和特征条件概率 ,常用方法为极大似然估计,通过训练集样本的统计信息直接推导概率参数。
1. 先验概率 的估计
先验概率表示类别 在训练集中的占比,通过计数法即可完成估计,公式为:
其中 为指示函数,当 时取值为 1,否则为 0, 表示训练集中属于类别 的样本总数, 为训练集总样本数,该估计逻辑本质是通过样本频率近似概率。
2. 特征条件概率 的估计
特征条件概率的估计需根据特征类型(离散型/连续型)分别处理。若特征 为离散型,取值集合为 , 为特征 的取值个数,则通过统计类别 中特征 取 的样本占比估计,公式为:
分子为训练集中属于类别 且特征 取 的样本数,分母为类别 的总样本数,同样通过频率近似概率。
若特征 为连续型,常用两种处理方式:一是特征离散化,将连续特征划分为若干离散区间,再按离散型特征的估计方法计算概率;二是分布假设法,最常用的是假设给定类别 时特征 服从正态分布,通过训练集中该类别下的特征数据计算分布的核心参数(均值和方差),进而确定特征取某一数值时的概率,无需复杂公式,核心是用数据的统计特征拟合合理分布来估算概率。
算法应用与分析
朴素贝叶斯的典型应用包括垃圾邮件过滤、文本分类、情感分析、医学诊断和推荐系统等,核心优势在于计算高效、对数据需求低,对异常值和缺失值具有一定鲁棒性,且能容忍无关特征。其局限性主要是依赖特征独立性假设,现实中多数特征存在相关性会影响分类精度,对稀有特征敏感,且概率估计偏保守,更适合类别判断而非精确概率估计。
任务:基于泰坦尼克号数据集的朴素贝叶斯参数估计
本次实训使用预处理完成的泰坦尼克号生存预测数据集,数据格式为NumPy ndarray(全数值型,无缺失值),无需额外处理数据,直接基于该数据实现算法。
数据的基本信息如下:
特征矩阵 X:shape=(n, 5),n为样本数,5个离散特征(对应讲义中的)。标签向量 Y:shape=(n,),类别取值为{0, 1}(0=未生存,1=生存,对应讲义中的)。数据类型:X.dtype=int64,Y.dtype=int64,无字符串或混合类型。
预处理后的5个特征均为离散型,取值范围固定,具体如下:
| 特征索引 | 特征名称 | 物理含义 | 离散取值 | 取值说明 | | 0 | pclass | 船票等级 | 1, 2, 3 | 1=一等舱,2=二等舱,3=三等舱 | | 1 | sex_encoded | 性别编码 | 0, 1 | 0=男性,1=女性 | | 2 | age_group | 年龄组 | 0, 1, 2, 3 | 0=儿童(≤12岁),1=青年(13-30岁),2=中年(31-50岁),3=老年(>50岁) | | 3 | family_type | 家庭类型 | 0, 1, 2 | 0=单身(无亲属),1=小家庭(1-2名亲属),2=大家庭(≥3名亲属) | | 4 | embarked_encoded | 登船港口编码 | 0, 1, 2 | 0=南安普顿(S),1=瑟堡(C),2=皇后镇(Q) |
以下是前5个样本的X(特征矩阵)和Y(标签向量)示例,直观展示数据格式:
| 索引 | pclass | sex_encoded | age_group | amily_type | embarked_encoded | survived | | 0 | 3 | 0 | 1 | 1 | 0 | 0 | | 1 | 1 | 1 | 2 | 1 | 1 | 1 | | 2 | 3 | 1 | 1 | 0 | 0 | 1 | | 3 | 1 | 1 | 2 | 1 | 0 | 1 | | 4 | 3 | 0 | 2 | 0 | 0 | 0 |
给定上述预处理好的X(特征矩阵)和Y(标签向量),请基于朴素贝叶斯理论,补充实现实现先验概率估计函数、条件概率估计函数和单样本预测函数。
数据实验楼"人工智能的数学基础与Python实践"实训项目重磅上线
登录网址:http://idatacoding.cn
项目目标:帮助学生建立 AI 数学基础知识与 Python 实践的关联,将抽象的数学概念转化为可操作的代码实现,解决理论理解困难的核心问题。引导学生通过 Python 编程实践,完成 AI 数学知识(如线性代数、概率论等)的代码落地,掌握用编程工具验证数学逻辑的方法。借助真实数据集的处理与可视化输出,让学生直观观察数学模型在实际场景中的运行结果,深化对 AI 数学原理应用价值的认知。培养学生运用 “数学理论 + Python 工具 + 数据验证” 的综合思维,具备独立用编程解决 AI 数学相关基础问题的能力,为后续 AI 学习奠定基础。
锻炼能力:线性代数; 概率论与统计学; Python实践
实践工具:Numpy; Matplotlib; Scipy; Pandas; Sklearn
前置基础:Python基础; 微积分基础; Matplotlib基础
项目介绍:数学是 AI 的底层逻辑支柱,动手编程则是 AI 能力落地的关键桥梁。本项目的主要目的是帮助学习者在这两方面进行融会贯通。项目通过 Python 代码实现、案例演练帮助学习者具象化理解人工智能中涉及的抽象数学基础理论,系统掌握AI的数学基础知识。具体包括以下五大模块:
向量与矩阵:AI 数据的数学表达。本模块介绍向量和矩阵的基本知识。向量部分我们先从其数学定义和Python表示开始,依次介绍向量的线性预算、向量内积、向量范数等。矩阵部分先介绍其定义和Python实现,讲解矩阵转置及其性质、随后介绍矩阵乘法、矩阵向量乘法。最后介绍矩阵乘法的两个重要应用:批量计算向量内积和余弦相似度。梯度下降:AI 模型的参数学习。本模块先介绍函数的导数和梯度概念,进而讲解梯度的数值计算方法。介绍完梯度的基本概念后,以线性回归这个简单问题为例,帮助学员构建AI模型中的损失函数的概念。通过对损失函数最优化问题的求解,自然引出梯度下降法的原理和过程。概率分布与贝叶斯推断 :AI 的不确定性建模。本模块主要讲解常见概率分布特性与贝叶斯定理推导逻辑。我们首先介绍随机变量、概率分布、期望和方差等基本概念。然后介绍了离散分布(伯努利分布、二项分布、类别分布和多项分布)、连续型分布(均匀分布、正态分布、指数分布、对数正态分布、学生t分布和贝塔分布)。随后介绍已知分布生成样本的方法以及基于样本和分布的参数估计方法。在贝叶斯推断部分,我们先讲解贝叶斯定理、然后介绍条件独立性假设,最后介绍朴素贝叶斯分类算法。最后我们介绍基于贝叶斯推断的极大后验估计方法。矩阵分解与降维:高维数据的压缩与提取。 本模块先讲解特征值、特征向量、协方差和协方差矩阵等基本概念。然后介绍特征值分解,以及基于特征值分解的PCA算法。随后介绍如何基于PCA进行数据降维、高维数据重构和图像降噪。最后我们讲解了奇异值分解及其在图像压缩中的应用。在讲解数学原理的同时,依托 NumPy 开展实践操作,帮助学习者掌握高维数据压缩与特征提取技术。优化算法进阶:让 AI 学得更快更稳。 本模块主要讲解突破上述局限的一些高阶优化方法。我们先讲解动量法、RMSprop 算法和 Adam 等进梯度下降法的改进算法。随后我们介绍过拟合的概念,以及正则化这种解决过拟合的优化策略,包括 正则化、 正则化和弹性网络。

项目截图展示:


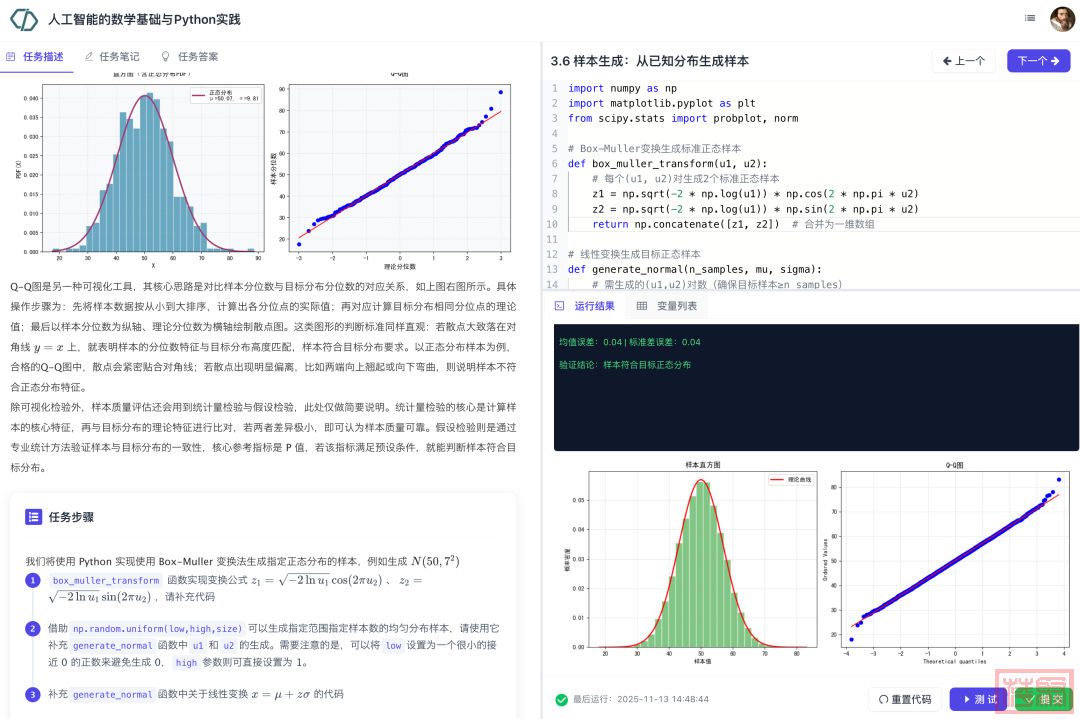



教师申请试用方法:
请联系微信加电话 136-9329-0406 开通项目权限
|
|